クワガタムシ2創作レポート
第一回(2002.6.29)
大好評?創作レポートシリーズ第2弾は
クワガタムシ2だ。例によって、これを書いてる
時点では
折れる目処はまったくたっていない。
見切り発車上等である。また、題材にクワガタムシを
選んだのは、単純に、今なら前作よりよいものが
できるだろうという根拠のない自信からである。
根拠のない自信これ最強。
さて、クワガタ2を折るにあたって、まずは前作
クワガタムシの見直しから始めようと思う。
なにしろ、前回のカマキリ2の創作レポートは
完成を急ぎ過ぎた。今回は、たとえ作品が完成
しても、できるだけ得意の駄文で引き伸ばす方針で
やっていくことにする。
というか、前作の見直しだけで3週間は引っ張るつもりだ
ともあれ、前作クワガタムシをご覧いただこう↓。


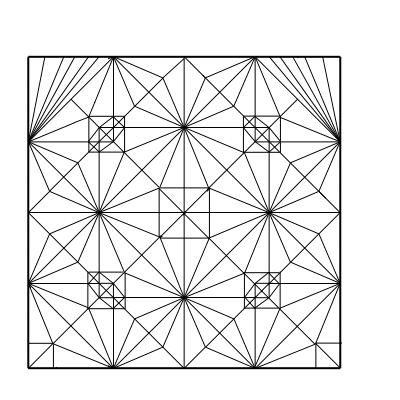
これはこれでまあ悪くはないけど、
今みると、結構、難点がいくつか目につくので、
あえて列挙してみる。
1、中脚が内部カドなので、折りにくい。また、
脚の太さが前、中、後で、不均一である。
2、長方形を敷き詰めるような配置になっているため、
4つの小さなカドの中央にあらわれる小さなカドを
つぶすことになり、非効率である。
3、比率が微妙すぎてわかりにくい。
主に気になるのはこの3つくらいだろうか。
パッと見、スタイルはそれほど悪くない。
脚の折り出し位置はちょっと実物とちがうけど、
触角や口、顎のトゲなどがちゃんと折れてる
点などは、まあ評価してやってもいいと思う。
これらよいところは極力踏襲しつつ、上に
挙げた3つの難点を解決するモデルをクワガタ2
の目標とする。即ち以下のような条件を満たす
ものである。
1、脚は全て辺、もしくは頂点からの折り出しと
して太さを均一にする。
2、余領域(カドにも帯にも使われない領域
(S太郎の勝手な命名))を腹などの厚みが
必要なカドに上手く吸収させて、折りやすい
形を実現する。
3、わかりやすい比率、折りやすい基本形。
4、触角、顎のトゲ、小楯板、背の割れ、口など
の表現、細く長い脚。しまったボディ、そして、
大きすぎず、小さすぎない魅力的なヒップ。
果たして、私がこれらの条件を満たす作品を
折ることは可能だろうか。もしできなかったとしても
そのときははじめから無かったことにしてしまえば
いいさ。
(適度になげやって次回につづく)
第二回(2002.7.8)
Yeah! やっと、ホリデー
探偵団マガジンをひらくのじゃ
すんげえ すんげえ すんげえ すんげえ 折り図
すんげえ すんげえ すんげえ すんげえ 蛇腹
山! 折り! ―・―!(ダッシュ、ドット、ダーッシュ!)
というわけで、第2回である。オリオリな夏希望。
さすがに前回書いた「見直しだけで3回延ばす」
というのは妄言だ(馬鹿か俺は)。
今回から、クワガタを折る上で課題となりそうな
部分をどのように折るかの検討を始める。
まずは、実物の形状を確認する。
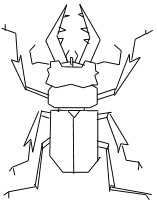
図は図鑑をみながら筆者が描いたクワガタムシである。
このような形を折るために特に課題となりそうなのは、
1、アゴのトゲをどう折るか。
2、背の割れ、小楯板をどう折るか。
3、頭、胸、腹の3段に分かれた形をどう折るか。
4、脚の折り出し位置を正確にするための構造をどうするか。
の4点だ。今回は1について考える。
1、アゴのトゲをどう折るか。
これは、実はクワガタを折ると決めた時点でアイデアだけ
は考えていた。それは、
「アゴのカドを半内部カドとして折って、付随した袖状の
部分でトゲを折る」
というものだ。円図、展開図略図を示すと、以下のとおり。
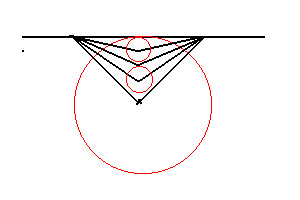
これを試しに折ってみると、下の写真のような形になった。
最終的にどのような形で折るか、細かい部分は未定で
あるので、このようなやりかたでトゲが出ることが
確認できただけでよしとする。

ちなみに、前作のクワガタでは、以下のような、
目黒氏のとぶクワガタムシで用いられているのと
ほとんど同じ方法を採用していた。
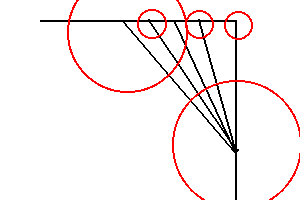
この方法は折やすく、非常に理にかなった方法である。
しかし、カド位置がこの位置にほとんど限定されてしまう
という特徴もある。
対して、上記の半内部カドを用いる方法だと、やや折りにくい
ものの、配置の自由度が若干いい。例えば、以下のような
配置ができる。
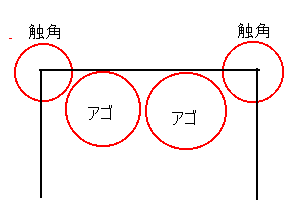
これは折るまえから見当がつくことなのだが、
アゴ2本に触角2本、脚6本と、計10もの
カドを辺に配置しようとすると、当然内部領域が
あまりがちになる。その意味で、比較的、細く折る
必要のないアゴのカドを内部におしやって、
辺の領域を他にゆずるのは合理的である。
また、もっとも細く折りたい触角のカドを用紙の角
付近からだせるのも理想的だ。
蛇足ながら、カドの紙厚のことはカドを折るのに
使われる紙の幅を確認するとよくわかる。
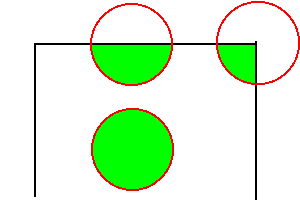
上の図より、同じ長さの普通のカドであれば、
必要な領域、つまり紙厚は、
内部:辺:角=1:1/2:1/4=2:1:1/2=4:2:1
となるのである。(第2回終り)
第三回(2002.7.14)
牛鮭定食を食べるときは、牛皿に紅ショウガを入れるのを
忘れるな俺!第三回。
前回は、アゴのトゲを折る方法を考えた。
若干説明不足気味だったので、トゲ3つ版の
途中写真をもう少し追加しておく。




さて、今回は、順番に従うなら、
「2、背の割れ、小楯板をどう折るか。」をやるはずだった。
しかし、アゴから背に進むまえに、口のヒゲ?をどう折るか
ということが以外に考えどころなので、それを先に考えてみる。
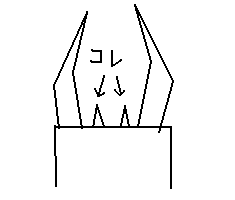
1.5 口ひげをどう折るか
前作のクワガタでは、口ヒゲは22.5度の素のカドの
先端をつぶしてできるヒダをつかって折っていた。
円図に示すと以下の左図である。
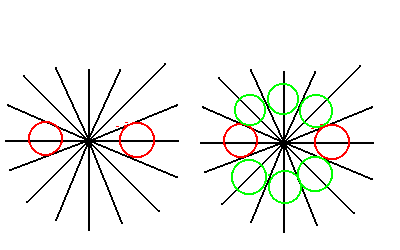
しかし、この方法では、右図にしめしたように、
本来もっとたくさんのカドが折れるし、それを
利用するのが普通である。
同等のカドが8個も折れるのに、6個つぶして2個しか
使わないのでは、とてもスマートとはいいがたい。
進歩がなければバージョンアップとはいえないので、
今回この方法は不採用とし、新たに構造を考え直すことにする。
まず、単純に円図をかくと、以下である。

円と円の間は、カドを中心線に平行にするために
すこし空けている。これに、仮に最低必要そうな45度
単位の線を描いてみる。
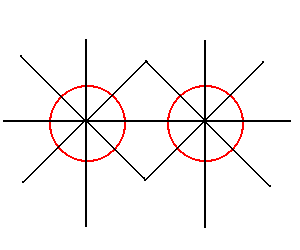
この形から真っ先に連想するのは、たとえば、
蛇腹的に折る方法(下の左図)や、よく使われる
下の右図の形などがある。
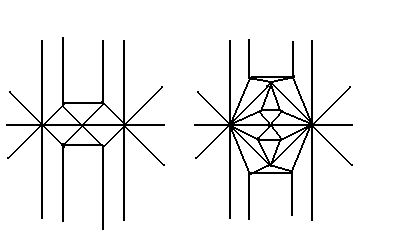
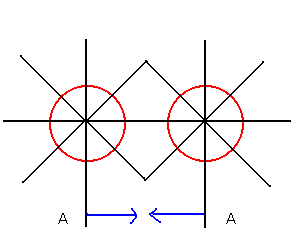
しかし、ここで問題が生じる。それは、
いずれの方法も、図のA線が中央に引き寄せられる
ために、中心付近にヒダ、もしくは、割れが生じてしまう
ということだ。
これがなぜ問題かというと、口のすぐ下
に控える頭部に、このようなヒダもしくは割れがあるのは、
造形上不満があるからである。↓
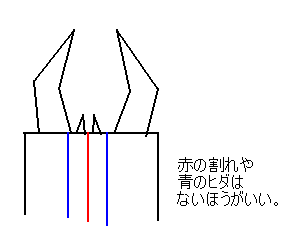
どのような方法で折るにしろ、二円の頂点を中心線に
引き寄せる限りは、縦方向の成分をもったヒダが
できるのは不可避である。では、この問題はどう解決すべき
だろうか。これには、様々な方法が考えられるが、
ポイントになるのは、
「ヒダの幅を大きくする」
ということだろう。ヒダの幅が大きくて頭部の幅をこえて
いれば、ヒダは問題ではなくなる。
例えば、先に示した蛇腹系展開図でヒダの幅を広げる
ということを実直にやれば、図の形になる。
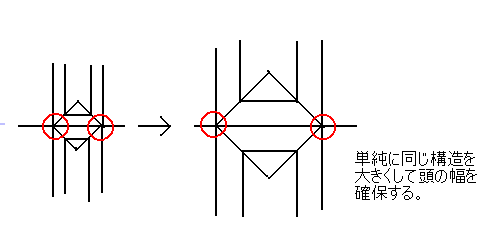
しかし、この方法だと、円の間が空き過ぎる
ので、若干、変形に技術がいるし、長く出せるはずの
カドの先端部分しかつかわないのは、やや非効率と言える。
では、例えば、ヒダを広げるのに、蛇腹的に幅を変換していく
構造はどうだろうか?
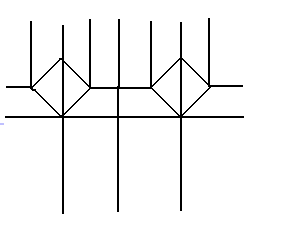
もちろんこれでも折れるけれど、ちょと泥臭過ぎて、
男の折り紙、という印象だ。
もっとスマートに折る方法はないのか?もちろんある。
たとえば、先の図で、A線を分子境界として用いたが、
これを下図のように、B線まで広げるという方法はどうだろう。
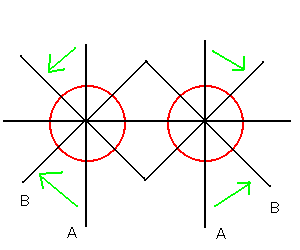
ヒダを広げるということは、つまりは分子境界を大雑把に
するということともいえるのである。それで、これを
洗練すれば、例えば以下の展開図がえられる。
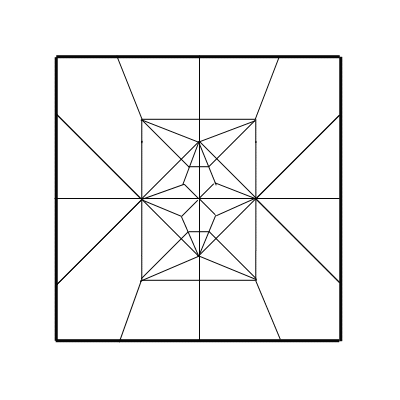
さらに、これを折ってみれば、下の写真のような形になる。

みておわかりのように、この形はかなり見立てがよい。
ほとんどそのままでもクワガタの頭部に見えるくらいだ。
最終的にこのままの構造で使うかはわからないが、
暫定で採用とすることにする。また、この形は、
カブトムシの小角(後角?)と頭部を折るときにも
きっと使えるだろう。
というのは、カブトムシの頭部を折るときも、
以上のようなヒダや割れをどう処理するかということが
同様に問題となるからだ。そのうち折るであろう、
カブトムシ2でもこの方法を採用したみたいと思う。
ところで、先ほど、AからBまで分子境界を広げる。
ということをやった。どうように、Cまで広げたら
どうなるか?と考える人がいるかもしれない。
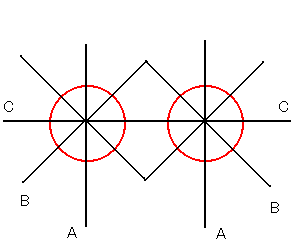
結論をいうと、目新しい構造にはならないのだけど、
色々考えてみるのも面白いと思う。
(第三回終り)
第四回(2002.7.22)
クーワガタァ折りたい奴ァ俺んとこへ来い!
俺もおーるけどしーんぱーいすんなー第四回。
さて今回は、「背の割れ、小楯板をどう折るか?」が
テーマである。クワガタに限らず、カブトムシその他、
あらゆる甲虫で必要な形状なので、重要な考えどころと
いえるだろう。
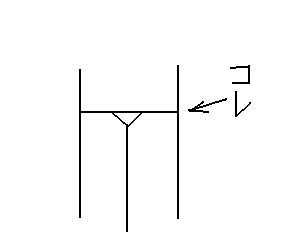
このような形を折るのに一番とっつきやすいのは、
変形技術を駆使する方法だろう。例えば、以下は
鶴の基本形から筆者が折ったクワガタの断片のような
ものである。

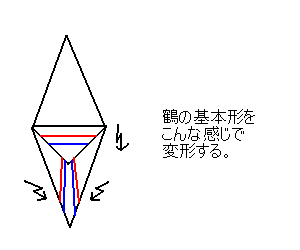
鶴の背の小カドから、小楯板を折り、割れは段折りで
再現したわけである。割れを段折りで折るのは、
背の立体も同時に作れて、合理的な方法なのだが、
もし腹のカドが内部カドだった場合、厚みで段折りが
しにくいという難点もある。実際、今回のクワガタは
腹は内部カドの予定なので、次に、基本形自体に
構造的に背の割れのシルエットを作る方法を考えたい。
まず、先ほど示したように、割れは段折りで以下のように
作れる。
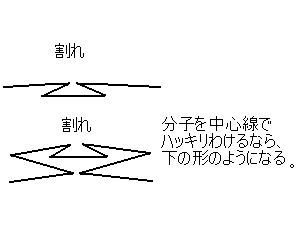
割れをつくるには他の方法もあるのだけれど、今回は
この方法をつきつめて考たい。それで、先の図を平行な
折り線として示すと以下である。
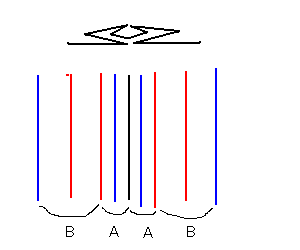
Aのヒダが内部に閉じ込められる必要性から、
Aの幅≦Bの幅
の条件がわかる。今回は単純な形として、Aの幅=Bの幅の
場合で話をすすめるが、もし構造が複雑になってきた場合、
この条件を意識することは重要と思う。今、折り線が平行の
場合を考えたが、必ずしも平行でなくてもよいので、
考えられるパターンを列挙してみる。
1、折り線が平行の場合
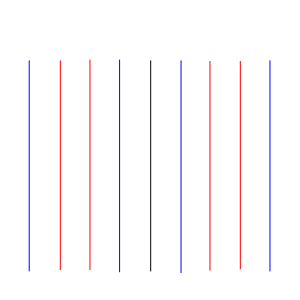
これは普通の蛇腹である。小楯板のカドを組み込むと例えば
以下の形が得られる。
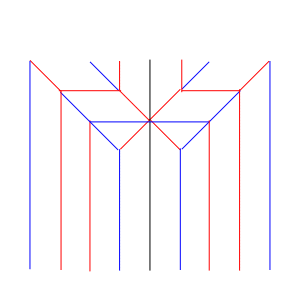

特に必要なところのみ折ったもの。

段折りで小楯板を折る。
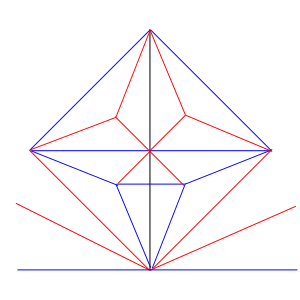
2、折り線が下すぼみな場合
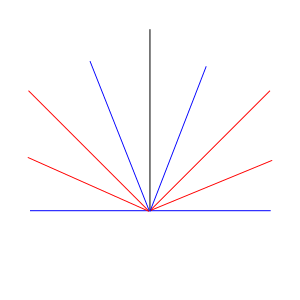
これは、腹にあたるカドが普通のカドになる。
小楯板のカドを組み込むと、たとえば以下のような
ビバの前川氏のカブトムシに使われていた形になる。
(この方法は前の私のクワガタでもパクって使ってある)
3、折り線が上すぼみの場合
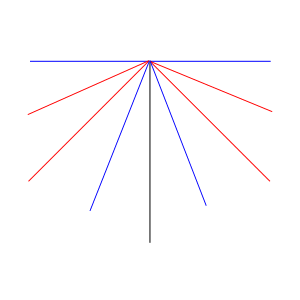
ちょっと変則的だけど、折れないことはない。
たとえば、以下の形が得られる。
以上3つ考えた中で、今回は1の平行なパターンを採用する
可能性が高そうだ。
理由は、背のカドの構造の両脇の余領域を吸収するのに、
平行な蛇腹が都合がよいからなのであるが、このことについては
全体の配置を考えたときにもう少し詳しく述べるかもしれない。
ともあれ、1を使おうと思って構造をながめると、一つ、
特に問題になりそうな点がでてくる。それは、割れを作るために
作ったヒダが、普通に使われている蛇腹と山谷反対になっている
ため、このままでは下方に配置する予定の脚のカドと
接続が困難であるということだ。この点を解決して
おかないと、安心してこの構造を使うことに踏み切れない。
では、どうしたらよいか。答えは、山谷ひっくり返っているのだから、
また、山谷ひっくり返し直せばいいのである。山谷が入れ替わる
ような構造といわれて、折り紙者がまずおもいつくのは、おそらく
中割り折りではないだろうか。以下に蛇腹の中割り折りを
示す。
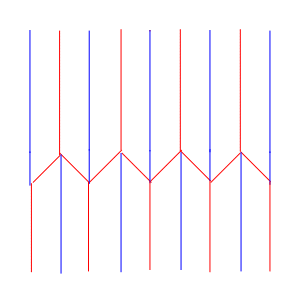
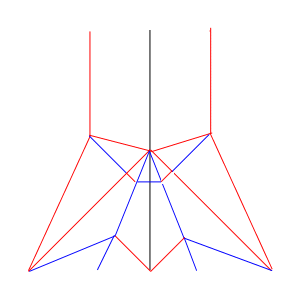
これを考えかたの基本として、1の下方の構造を定めると、
例えば以下の形になる。(山谷が本来の形に変換されている)
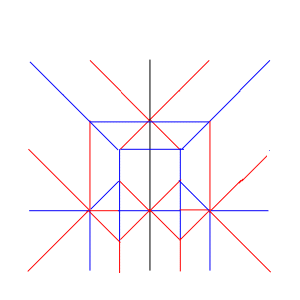

たたみ方の途中図
この形までたどり着けば、脚のカドを接続するのは
それほどむずかしくないだろう。以下に、脊髄反射的に
適当に折ったものの写真を載せておく。

ビバ!適当!

あられもない姿だ。
もちろん、この形のまま使える保証はないけれど、
大雑把であっても折れることが確認されることには
意義があるのである。
(第四回終り)
第五回(2002.7.29)
いやー。なんか、あんますっとろいことやってらんない
雰囲気になってきたなあ。でも、マジ、ガチンコで同時進行
なんで、今回も出来たところまでです第5回。
今回は、脚の折り出し位置をどうするかがテーマである。
折り紙では、昆虫の6本脚は、同じ付け根から折り出される
ことが多い。ところが、実物は必ずしもそうはなっていない
ので、それを極力正確に再現しようというわけである。
そのためにまずは下図にてクワガタの脚の出方を確認する。
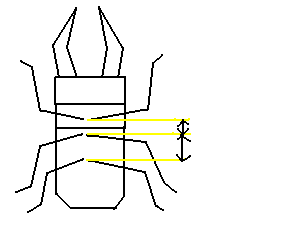
図に示したように、クワガタでは、前脚と中脚は胴と腹の
間の節を挟んで、かなり近い位置から出ている。それに
対して、後脚は、それらから結構はなれてたところから
生えている。また、上アゴの付け根部分から、前脚の付け根
までの間には、頭と胸があり、かなり隔たりがある。
さらに、アゴの長さは、脚の長さよりもやや短いということ
も確認できる。そこで、これらのことを基本枝構造にしてみる
と次のようになる。
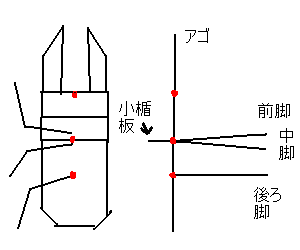
前脚と中脚は、接したカドからでもほとんど差し支えないだろう。
頭部などをどのようなカドで折るかは未定であるけれど、
前脚と中足の付け根付近は胸と腹の間であるので、
その付近に図のように小楯板のカドを出せれば理想的だ。
実際私は、基本枝構造をあまり書かないのであるけど、
ともかくこの図のようなことを考えつつ、円配置を考えると、
だいたい以下のような形が得られた。
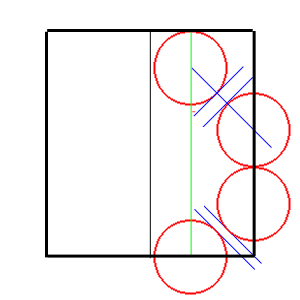
この図で特に着目すべき点は、図の緑の線で示したように、
上アゴの中心と後ろ脚の中心が、垂直方向の線で関連づけ
られているということだ。このような形をつくったのには、
複数の理由がある。まず第一に、この線によって、中央に
蛇腹的平行線の要素がつくれる。これにより、前回考えた
背の構造が埋め込みしやすくなる。また、この線の近傍の
内部領域は、カドに使われない余った領域であるので、
これを吸収するのに、蛇腹はもっとも適している。
またさらに、アゴのカドを脚より短く折るために、
下図でしめすような小円によるカド長の侵食が実現できる。
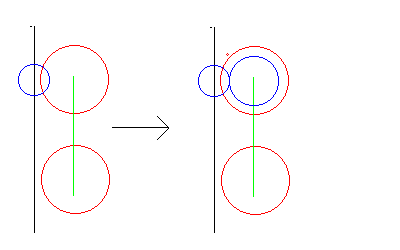
上アゴが正中心に対して平行に折られるのにたいして、
後ろ脚は垂直でかまわないことから、両者の長さに違いが
作れるわけである。このような考え方は、カマキリ2の
触角のときにも用いた。分かりやすい構造で微妙な長さの
比を作りたいときには、カドの侵食による方法は非常に
有用であるといえるだろう。
ともあれ、これを比率適当、内部の折り方も適当で、
大雑把に洗練すると、だいたい以下のような形になった。
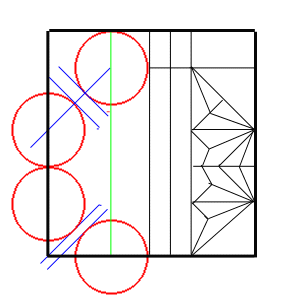
さらに、これを折ると次のようになった。基本枝構造と
比較してみて欲しい。


偶然(ホントは確信犯だけど)小楯板のカドが折れている
ので、さらにもう少し細かい部分を造形してみると、
下のようになる。


比率は未定であるが、だいたい欲しい脚の出位置が得られた。
小楯板として折る予定のカドが折れているので、次に、
この部分に前回考えた割れの構造が組み込めないか考える。
洗練した展開図は分子境界が縦方向にまっすぐなので、
その形で折れるように、前回の背の構造を折ると、次の形になる。
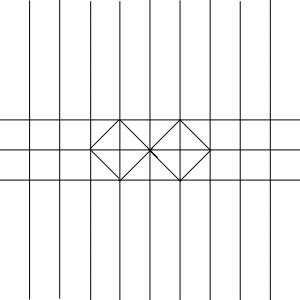

ここで問題となるのは、矢印で示した割れの側に現れる
ヒダである。このヒダは、例えば小楯板のカドに吸収させて、
この方向にでないように折ることもできる。しかし、
それだと小楯板のカドの紙厚が厚くなりすぎてしまう。
であるので、このヒダは基本形の方で吸収させた方がよい。
で、考えた結果、以下のように折って、前脚の付け根に
挟み込む形で吸収させるのがよさそうという結論になった。
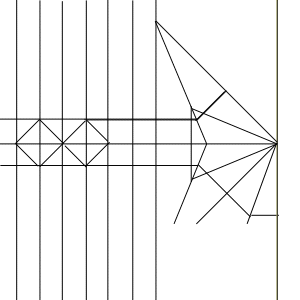
さらに、実際にさっきの基本形に組み込んだのが以下である。


前脚の付け根は若干紙厚がますけれど、別に折るのに支障が
でるほどではないので、これで御の字だ。
また、下方の後ろ脚との接続は、前回考えた構造を組み込めば
できることがわかっているので、皆まで折らなくても、
これでほとんど埋め込み完了である。
つまり、比率適当ながらも、胸から下の後半身はだいたい
折り方が決まったといえる。残る課題は、頭部、
それと後半身の接続、頭の段々をどうするか、全体の比率の
決定などであるので、次回以降でこれらを"じっくり"考えたい
とおもう。
(つーか、昆虫で早折り合戦なんてやったらマジ体壊すと思う)
(第五回終り)
第六回(2002.8.5)
第六回。
結果を先にいうと、週末必死こいて取り組んだので、
一応完成はした。しかし、その過程のレポートを
書く余裕がない。そもそも、頭部の創作を残した上、
全過程の中でもっとも考えどころである全部品の
統合、洗練化、比率決定を一回のレポートで述べる
事自体が難しい。そこで、そのへんのところは
もうザックリ省略して、出来上がった展開図と比率、
基本形、及び試作をみていただくことにする。
まずは展開図。↓
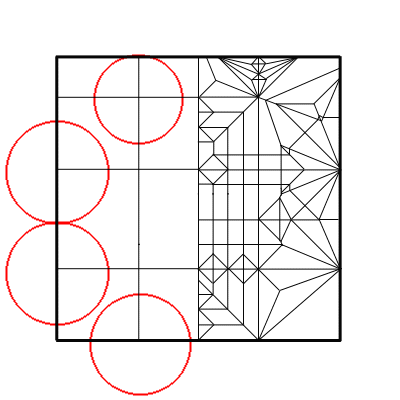
背の割れ構造と
半内部カド
の処理が案外
入り組んで
いるので、マニアでもそれほど
簡単にはたためないだろう…
などと言ってみる。
ていうか、第三回でやった内部カドからの
ヒゲの折り出しつかってないじゃん俺。
(ヒゲは辺部分から折っている。)
まあ、同時進行だからそういうこともあるさ。
次に、比の取り方。
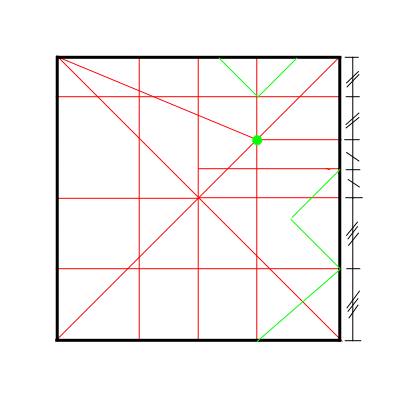
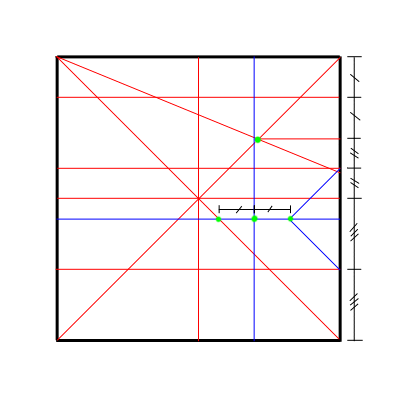
注)上の比は前脚と中脚の
間の構造に不整合があるので、
その点を改善したものが
この比です。(2002.8.6追加)
手順がちょっとだけ増えますが、
こちらのほうが断然スマートに
折れますので、挑戦される方は
こちらで折って下さい。
さらに、基本形段階↓
 表。背の割れと小楯板、
表。背の割れと小楯板、
背の段々が構造的に組み込まれ
ている点に着目して欲しい。
 裏。
裏。
 横。すべてのカドと帯が、ほぼ
横。すべてのカドと帯が、ほぼ
あらかじめ設定した基本枝構造
どおりなので、胴の段折りなど
が必要ない。
そして、以下が試作。

紙を買いにいく暇がなかったので、イキがって26cm
百円折り紙で折ったら仕上げがかなりキツイことに。
しかし、このサイズで折ればわりと実物大に近くなるようだ。
つうか、このメーカーの折り紙、汗ですぐぼろぼろに
なっちゃうんだよなあ。百円だから文句はいえないか。
ちゃんとした作例を次回までには折りたいと思う。
(まだつづくのかよ)
気が向いたらまた見にきていただきたい。
(第六回終り)
第七回(2002.8.12)
「俺は折り紙者同士で戦うつもりはないんだ!」
ファイナルベント第7回。
先日発表した作例写真と展開図(比率修正版)
を再度掲載。

さて、今回は前回省略した、頭部の創作過程及びそれと
後半身の接続についてかいつまんで述べる。
○頭部の創作
例によって円配置から考える。
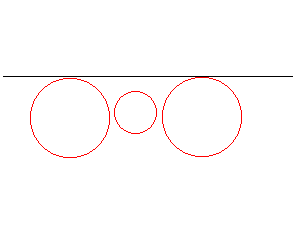
これは変にこだわらない限り簡単だ。
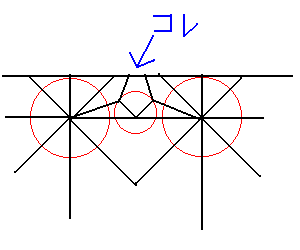
実際折ったものをみると、矢印で示した先の途切れた
形のカドは、口ひげを折るのにとても都合がよい。
そこで、もう第三回で一週間かけて考えた内部カド
からの口ひげの折り出しはもうザックリあきらめて、
この部分から口ひげを折ることにする。
これを折った形状がどうなるかは作例を参照されたい。
○後半身との接続
今考えた頭部の展開図と先々週考えた後半身の接続を
考える。試験的にもっとも単純に連結してみると
以下の形になる。
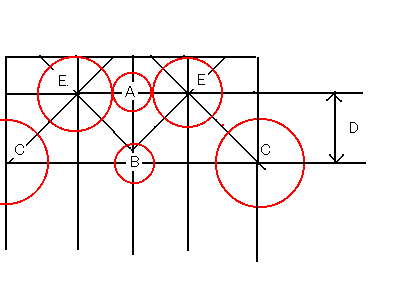
一見問題なく折れそうだけれど、実際折ってみると
バランス的な問題がある。それは、今、Cのカドは
Eのカドより大きくて、かつ、間に帯領域を挟んで
折り出されなければならない。というのは、大アゴ(E)
と脚(C)が同じ長さだと、若干脚が短い印象になり
がちになるし、帯がないと、アゴの付け根からいきなり
前脚が生えることになる。従って、条件を満たす形を
つくるためには、図に示したDの幅が十分大きい事が
必要である。ところが、これを大きくすると、構造的に
横方向に連絡のあるA(頭)のカドとB(小楯板)の
カドの間が広がりすぎてしまうのである。
この形を許したまま基本形を創出すると、頭と胸の間に
ある広すぎる領域を段折りで寸詰めるような操作が必要に
なってしまう。このような折り方は、胴のボリューム感
が出る利点などもあるので、一概に悪いとは言えない。
しかし、できるだけ基本形段階でのバランスが完成形に
近いというのが私の理想である。
そこで、このような場合は、まず、AとBの間は
必要量まで近接させて固定する。
次に、Cを大きくとるため、Cの中心をL線上を外側に
向かってずらす。
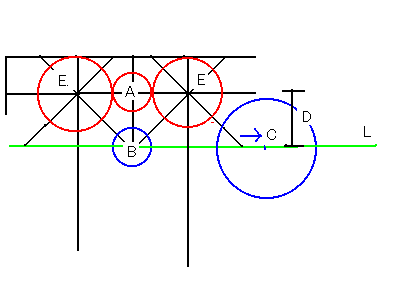
じつはこの操作は、全体の円配置をにらみつつ行っている。
先のCとEの中心が45度線上にのった形に比べて、
Cが外にずれる方が全体効率が良いという確認の上での
変形なのである。しかし、ここではその確認まで述べる
ことはしない。ともあれ、上図のCが外にずれた形では、
それぞれの円の中心が必ずしも22.5度倍角上に
のっていないので、何らかの洗練が必要である。
次にそれを考える。
○円の中心を結んだ線が定角にならない場合のあれこれ
このような場合の洗練というのは、洗練化の最も
根本的な問題の一つだろうと思う。というか、
私ごときが、かいつまんで述べるにはテーマが
大きすぎる。ここは、最終的に採用された形をふくめて、
いくつかの折り線パターンを提示する程度に留めたい。
1、今回採用されたパターン
二つの円がその中心が定角上にのらない形で
近接しているとき、私がまず考えるのは、
「どちらの円を素のカドで折るか」
ということである。
「どちらのカドは素のカドで折らなくてもいいか」
と言い換えた方が適当かもしれない。今回、大アゴと
前脚とを両天秤にかけて、大アゴは半内部だし
(内部カドは素ではないカドとして折られることが多い)
前脚のカドの方がより素のカドとして折りたいという
結論になったので、以下の図をまず描いた。
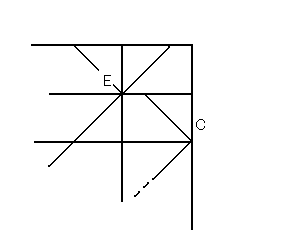
45度倍角線はCの中心から延ばし、Eで交わらない
形になっている。
これをみながら、ウーンと一声唸ると次の形になる。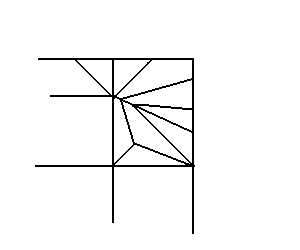
用紙角付近は折り線的に開放されているので、
適当に折っても触覚は折れるだろうという打算である。
これをもう少し変形すると今回採用した形になる。
1、今回採用されたパターン
二つの円がその中心が定角上にのらない形で
近接しているとき、私がまず考えるのは、
「どちらの円を素のカドで折るか」
ということである。
「どちらのカドは素のカドで折らなくてもいいか」
と言い換えた方が適当かもしれない。今回、大アゴと
前脚とを両天秤にかけて、大アゴは半内部だし
(内部カドは素ではないカドとして折られることが多い)
前脚のカドの方がより素のカドとして折りたいという
結論になったので、以下の図をまず描いた。

45度倍角線はCの中心から延ばし、Eで交わらない
形になっている。
これをみながら、ウーンと一声唸ると次の形になる。
用紙角付近は折り線的に開放されているので、
適当に折っても触覚は折れるだろうという打算である。
これをもう少し変形すると今回採用した形になる。
2、今回採用されなかったパターン
1では、Cの角を素のカドとして折った。私はこのよう
なとき、「Cを尊重する」という言い方を勝手にしている。
そこで次に、「Eを尊重する」場合のパターンを考える。
すると、以下の図がまず描ける。
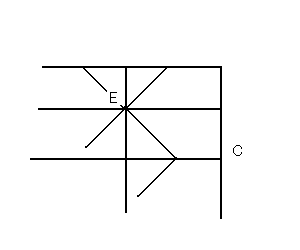
これをみて、ウーンウーンと二声唸ると以下が得られる。
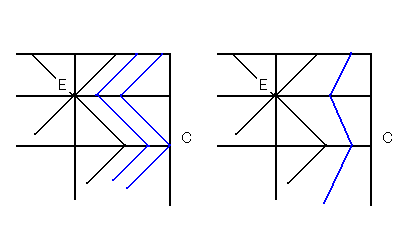
左に示したパターンは蛇腹的にCを延ばしたパターン
であるといえる。比較的Cが素のカドに近い形で
折れるのが利点だけれど、蛇腹線の比率決定や
実際に折るのが、やや小難しくなりそうだ。
たいして、右のパターンは、素のカドの先端を
突き合わせて侵食させたパターンと見て取れる。
このパターンはカド先端にボリュームがでるので
動物の脚などを折るのに適していると思う。(以下)
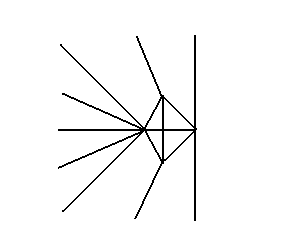
1、2と大雑把に述べてみたが、上に挙げた以外にも
折り方は人によって様々あると思う。
さて、頭部と後半身の連結は以上でだいたいかたづいた
とすると、基本形完成までに残る問題は比率決定だ。
しかし、これについてはもう本当に省略する。
概ねのやり方だけ言うと、まず円配置で最適なバランス
を決め、それに近くてかつ整合性があり、わかりやすくて
折りやすい比率が、天から授けられるのを祈り、求めるのである。
神に誠意を示すためには、水垢離くらいはする必要がある
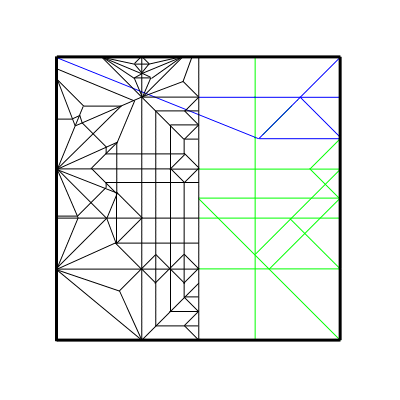
(かもしれない)。以下に完成形の展開図の円配置を
載せておく。特に、緑の線で折り線の関連づけを行い、
極力わかりやすい折り線パターンで折れるように
工夫してある点に注目されたい。
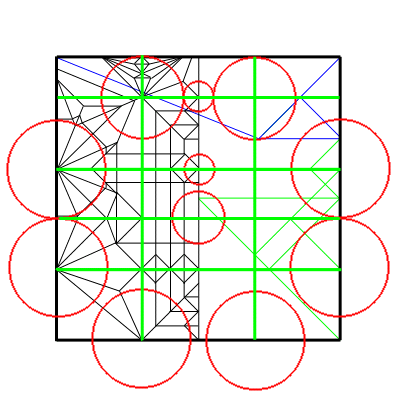
(クワガタムシ2創作レポート完)

























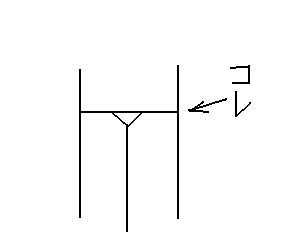


































 表。背の割れと小楯板、
表。背の割れと小楯板、 裏。
裏。 横。すべてのカドと帯が、ほぼ
横。すべてのカドと帯が、ほぼ













